Large Language Models (LLMs) these days can write essays, summarize research papers, generate recipes and travel itineraries, and debug your code — but ask ChatGPT to multiply two four-digit numbers, and it will fail over 90% of the time. [1]

Why? It turns out that numbers are quite different from other kinds of language! Numbers have specific meanings, but unlike letters or words, these meanings exist on a continuous scale with infinitely many values that operate under a strict and complex set of rules.

We shouldn’t expect LLMs to be perfect calculators. But there are nevertheless some compelling reasons why we might want to tackle the challenge of how to represent numbers in LLMs as we envision how the way we do science could evolve over the next 5-10 years.

For instance, how might science change if researchers had access to an AI model trained on a massive variety of scientific data? LLMs achieve a fluency with language-based tasks, even ones they weren’t explicitly trained on, because they were trained using an astounding amount of text data from diverse sources. As a result, they have opened up creative new ways to engage with text information. Would an AI model of such scale specializing in numerical data open similarly innovative paths of inquiry for scientists in the near future?

One key reason why we haven’t yet seen major models like this emerge is that scientific datasets come in highly specialized formats that require domain expertise to understand. Most of the so-called “foundation models” we see shaping the public’s experience of AI today are experts in a single data format: text, images, video, etc. Similarly, AI models in science today are carefully constructed to reflect the highly-curated datasets on which they are trained. A model spanning scientific domains, however, needs to be adaptable — as flexible as an LLM, yet grounded in a rigorous sense of numerics.

Every proposal for how to treat numbers in language models struggles with how to translate the infinite space of numbers into a finite number of vocabulary elements. LLMs break down language into pieces called “tokens”, sort of like tiles in a game of Scrabble. Adding numbers into the mix is like adding an infinite number of Scrabble tiles, making the game impossible to play. Additionally, no existing numerical tokenization strategy can effectively generalize outside the scope of numbers seen during training.

For this reason, we developed xVal: a continuous way to encode numbers in language models for scientific applications that uses just a single token to represent any number. This strategy has three major benefits:

• Continuity: It embeds key information about how numbers continuously relate to one another, making its predictions more appropriate for scientific applications.
• Interpolation: It makes better out-of-distribution predictions than other numerical encodings.
• Efficiency: By using just a single token to represent any number, it requires less memory, compute resources, and training time to achieve good results.

xVal works by treating numbers differently than other kinds of text inputs. Each number in a text dataset is pre-processed: its value is stored in a separate vector, and in its place, we leave a single token: `[NUM]`. We then encode the pre-processed text into a finite series of word tokens, but multiply the embeddings of `[NUM]` tokens by their corresponding numerical values. When the model is asked to decode a `[NUM]` token, it uses a dedicated token head in its transformer architecture trained with Mean Squared Error (MSE) loss to predict that token’s value as a scalar.

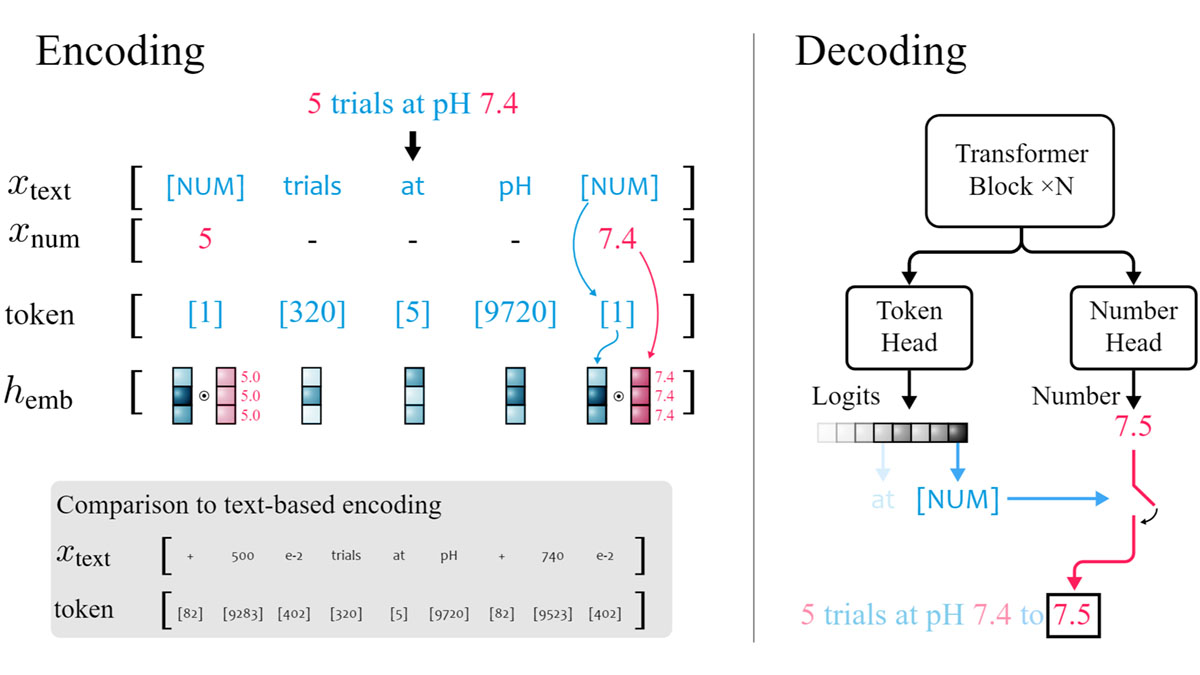
We ran a series of experiments to test how xVal performs on various datasets in comparison with four other numerical encoding strategies defined in [2] and summarized in the table below. These strategies range from encoding each digit of a number separately to encoding the entire number as a single token.

First, we evaluate these encoding schemes on simple arithmetic datasets, e.g. various combinations of addition and multiplication. We find that xVal outperforms the other methods on multi-operand tasks like `((1.32 * 32.1) + (1.42-8.20)) = 35.592`. In the notoriously tricky task of multiplying large multi-digit integers, it performs at about the same level as the other encodings and is less prone to large outliers in its predictions.

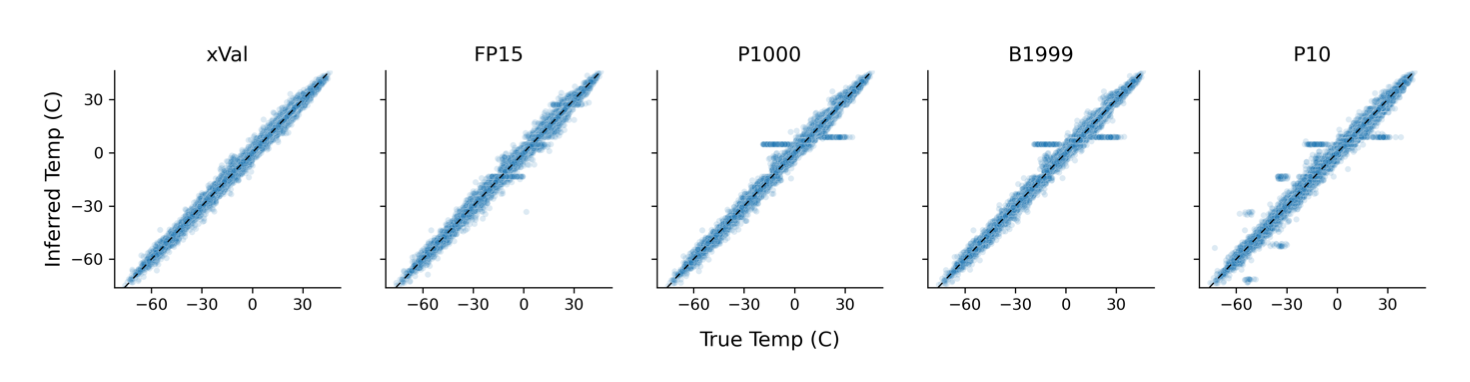
Next, we evaluate the same encoding schemes on a subset of the ERA5 global climate dataset [3] consisting of temperature readings from all over the world. In this setting, xVal excels due to its implicit bias towards continuous predictions. It achieves the best performance in the least amount of training time. xVal also avoids the pitfalls of over-predicting particular numbers due to imbalances of those tokens in the training data, as seen for the other encodings in the horizontal stripes in the figure below.

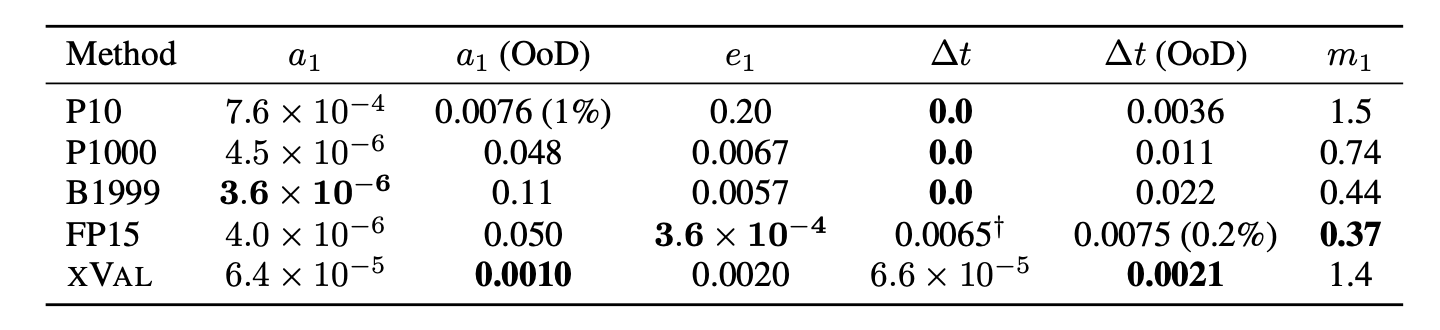
Finally, we evaluate the encoding schemes on simulations of planets orbiting a central mass [4]. Following training, we ask the model to predict the masses of the planets and qualities of their orbits: their semi-major axes a and orbital eccentricities e as well as the sampling rate Δt. Here, we see excellent interpolation by xVal: its out-of-distribution predictions are better than any other encoding scheme.

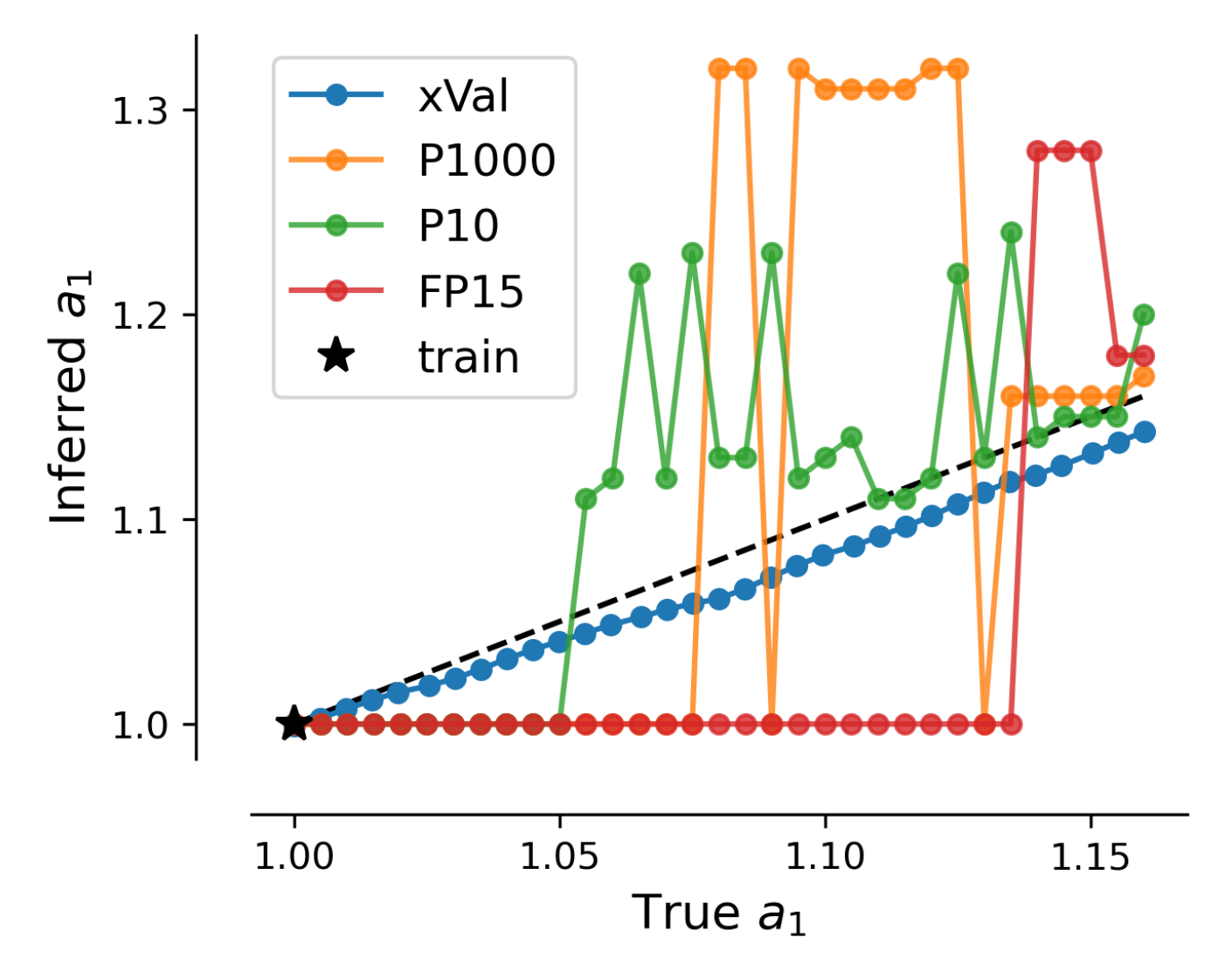
Looking more closely at its predictions, we can see that the implicit bias of continuity plays a key role in its interpolation abilities. In the figure below, we evaluate its predictions of an orbit’s semi-major axis. There is no sample in the training data with a ∈ (1, 1.16). Upon testing, only xVal successfully approximates these values continuously within this gap in the training data.

By efficiently enforcing continuity end-to-end for numbers in a language model, xVal is an innovation that could help enable future foundation models connecting multiple domains of science.

— Mariel Pettee