The Euler Characteristic
The Euler characteristic (χ) is a topological invariant of even dimensional spaces which provides information about the global structure of the manifold. For closed orientable two dimensional manifolds (surfaces) it basically just counts the number of handles of the surface, specifically if the number of handles is represented by g, the Euler characteristic is given by χ = 2 – g. So a sphere, donut and a 2 holed torus have Euler characteristics of 2, 0 and -2 respectively.
As a topological invariant, the Euler characteristic only cares about the global structure of the manifold, i.e. it does not care about the the specifics of the shape of the object. However, through the Gauss-Bonnet theorem, the Euler characteristic can be expressed as the integral of a local density over the entire manifold. The local density turns out to be the the Gaussian curvature but this is not so important for our discussion. The important point is that the Euler characteristic can be thought of as a global sum (integral) of a local quantity but it does not depend on the local shape of the object.
As an example, take a sphere with χ = 2. Now, slowly squish it so that it turns into a thick pancake. The Euler characteristic is still the same as before, but the local density has shifted around (it is more curved at the edges than in the middle) in such a way that the total sum of the local density is still 2.
The Euler Current
The situation above is very similar to any physically conserved charge. For example, if you place <i>N </i>electrons on a neutral conducting sphere, they can move around and redistribute themselves but the total charge on the sphere will always be <i>N. </i>In this situation, we can define an electric current which describes the movement of the electrons and there is a conservation law that relates the electric current to the change of the electric charge. In a sense, the global conservation of electric charge can be translated into a local conservation law if we include the electric current as well. This is possible because the object which is globally conserved (the total charge) can be written as a global sum over a local density which in this case is the local electric charge density.
In much the same, way we expect to be able to define a current for the Euler characteristic, i.e. as we deform a 2D surface, there should be a current that describes how the local density, the curvature, redistributes itself in such a way that the global topological invariant is conserved. And this is what we introduce in our recent paper.
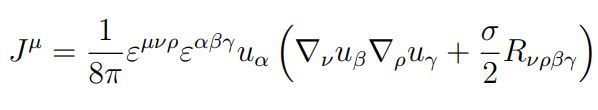
To define this current, we need a vector which tells us which direction is time in the 3-dimensional manifold. In the above formula u plays the role of time.
The Euler Current in Physics
We discovered this current in a round-about way, thinking about the description quantum Hall systems and graphene in particular. The effective theory describing quantum Hall systems includes a crucial Chern-Simons term. However, this term is not compatible with the emergent relativistic symmetries of graphene. So we were searching for an analog of the Chern-Simons term which is relativistically invariant. This is where the Euler current comes in and saves the day.
