Fractional Quantum Hall
The Hall effect, first discovered in 1879 by Edwin Hall, is a phenomenon in which a current carrying metal bar placed in a magnetic field will develop a potential differential called the Hall voltage which is perpendicular to both the current and the magnetic field. The relationship between the Hall volatge and the current is linear and the constant of proportionality is called the Hall conductivity (or resistance depending on how you define the ratio) and it depends linearly on the strength of the magnetic field. What this means is that if you fix the current in the hall bar and you increase the magnetic field, the Hall voltage will increase linearly as well. All of this is pretty straight-forward and can be explained using high-school level physics.
The quantum Hall effect, the quantum version of the classical Hall effect, is a lot more interesting. The constant of proportionality between the induced Hall voltage and the current becomes quantized because of quantum mechanical effects. So if we perform the same experiment as before, keeping the current fixed and increasing the magnetic field, we will see that the Hall voltage will stay fixed for a while (there is a plateau) but then jumps and the jump turns out to be integer valued (in units that are natural for the problem)! The plateaus of this experiment are the hallmark of the quantum Hall effect. The explanation of the quantum Hall effect is a little more complicated but well understood using undergraduate quantum mechanics and comes down to completely full vs. empty energy levels of an electron in a magnetic field which are called Landau levels.
The fractional quantum Hall effect (FQHE), is the yet more exotic incarnation of the phenomenon which takes place when the electronic energy levels are not completely full, hence the name fractional. Interestingly, the plateau of the FQHE appear at specific filling fractions of the Landau levels (most prominently 1/3). There is a whole zoology of different states and phenomena that appear at different fractions. It is fair to say that the FQHE is one of the more active and exciting fields of research in condensed matter physics at the moment.
The Magneto-Roton
One of the interesting properties of fractional quantum Hall systems is that they possess neutral excitations reminiscent of the roton in Feynman\’s theory of superfluid Helium. The strange thing about these excitations is that they carry more energy when they are at rest compared to when they carry a specific amount of momentum. This behavior is very intuitive from a classical perspective. There are a number of competing theoretical descriptions of this phenomenon. In our paper we focus on a very generic description of the system that can be applied to any theory.
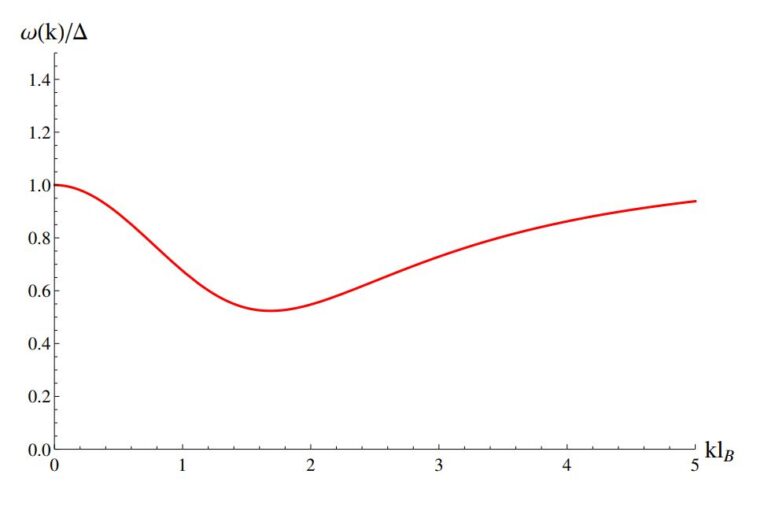
The details of the work are a little technical. We use a generic parametrization for the spectral densities associated to the expectation value of the energy-momentum tensor to find relationships between various physical properties of the system. These spectral densities can be described as the probabilities for absorption or emission of circularly polarized gravitons by the quantum Hall system. We also specifically construct a theory which realizes the magneto-roton as a mixing between oscillations of an internal metric and the hydrodynamic motion. In a way this model explicitly demonstrates a recent conjecture by Haldane where the magneto-roton at long wavelengths is associated with the quanta of the fluctuations of an internal metric (a graviton of sorts).