It’s not every day that you publish a paper with a title that could be straight out of Star Trek. So I’m really excited about this new work with my collaborator Savdeep Sethi, not just because the name sounds cool but because it is finally proving a relationship that my adviser Dam T Son and I conjectured to be true three years ago. I should perhaps mention that the gravitational anomlies that exist in quantum field theory are not at all what you would expect from pop culture, sorry to disappoint. But I still find them super interesting, so please read on! For the experts, the paper is published in JHEP (Journal of High Energy Physics) and the pre-print is available for free on the arXiv.
Here I will try to explain the concepts of the paper in as simple terms as I can. No equations!
Quantum Anomalies
So what exactly are quantum anomalies? It all has to do with symmetries. If a symmetry is present in the classical description of a system but is broken by quantum corrections, this symmetry is said to be anomalous. Technically, if a symmetry is broken classically and is restored by quantum magic, that is also called anomalous but this is a lot more rare.
Symmetries are very important in physics. They usually have deep consequences, for example spatial translation invariance implies momentum conservation. There are other symmetries that imply all sorts of things: energy conservation, electric charge conservation etc. Now, it should be clear why it would be a big deal if quantum mechanics breaks any of these symmetries. In practice, the symmetry that is usually broken is of the charge conservation type, e.g. you could have your electric charge disappearing or appearing out of nowhere. This would be an inconsistency that would render the theory pathological.
Global vs. Local Anomalies
Just like symmetries, anomalies are divided into two groups: local and global anomalies. Local or infinitesimal anomalies, are anomalies for transformations that can be infinitesimally small. For example a translation transformation can be as small as you want, you can translate by 1 light year, 1 cm, 1 nano-meter or anything you want. The parameter for the transformation can be taken to zero. Global or discrete anomalies refer to transformations that cannot be made small. Technically, one would say that they are not continuously deformable to the identity transformation (no transformation). An example of this is reflection, you cannot smoothly deform a reflected image to its original.
Quantum Gravitational Anomalies
Just like the other quantum anomalies, gravitational anomalies also pertain to a classical symmetry that is broken because of quantum corrections. Their presence, in simple terms, implies that the gravitational force cannot be consistently incorporated in the theory. In terms of conservation laws, it implies that the energy-momentum (EM) tensor is not conserved. Since Einstein’s general relativity is defined via the equation of the EM tensor of matter to the space-time curvature, the non-conservation of the EM tensor, makes this whole thing pathological.
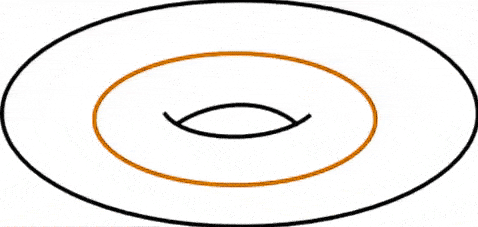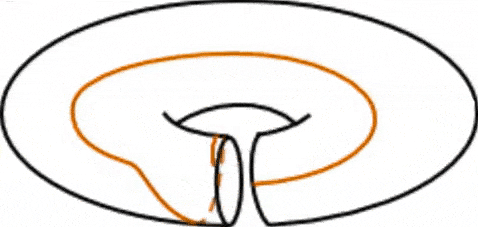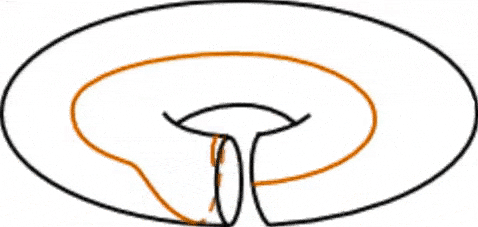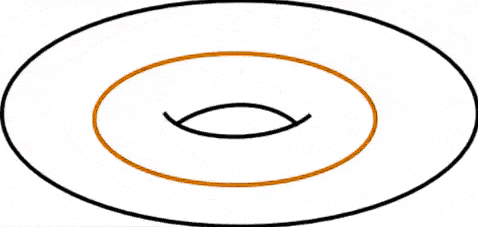
The global gravitational anomaly that we are interested in is called the Dehn twist: a global transformation which corresponds to cutting, rotating one side by 360 degrees and reattaching the twisted torus. Classically this transformation is a symmetry of the system, however, in the presence of a perpendicular magnetic field, this transformation can become anomalous.
So there you have it! The term “anomaly” is applied to many different things, but in the realm of theoretical high energy physics it has a very specific definition and can render some theories pathological while providing interesting consequences for others. In our case, we prove that in certain theories the Dehn twist is indeed anomalous and show that this anomaly has measurable consequences. In particular the part of the chiral vortical effect inherits one of its coefficients directly from this anomaly. In fact, we conjectured this relationship in a previous paper.
