Here at the university of Chicago, we have been thinking a fair bit about quantum Hall systems and their properties. One of these properties is the Hall viscosity and its relationship with a space-time defect called torsion. We recently put out a paper basically refuting a relationship between these two quantities claimed by other authors. We believe the source of the erroneous relationship is a simple misunderstanding of the exact definition of the Hall viscosity in the first order formulation of general relativity. The paper is in collaboration with Michael Geracie and Matthew M. Roberts, and is available on the arXiv.
I will not go over the details of the paper in this post but I think it’s a good opportunity to talk about the first order formulation of general relativity and how to avoid a common pitfall when analyzing the effects of torsion.
Second Order vs. First Order Formalism of General Relativity
The formulation of Einstein’s general relativity that is usually taught is in the second order formalism. What this means is that the primary actor is a dynamical metric and the various parts of the formulation (for example the curvature) are derived from the metric. This formulation of GR is nice because it is simpler and does not require a deeper knowledge of differential geometry, moreover it is perfectly sufficient for almost all practical purposes.
The one shortcoming of the second order formalism with the metric as the dynamical variable is that it does not allow for the existence of torsion. Indeed the Levi-Civita connection that relates the metric to the curvature is based on the assumption that the manifold has zero torsion. The cartoon below demonstrates torsional and curvature defects on a manifold.
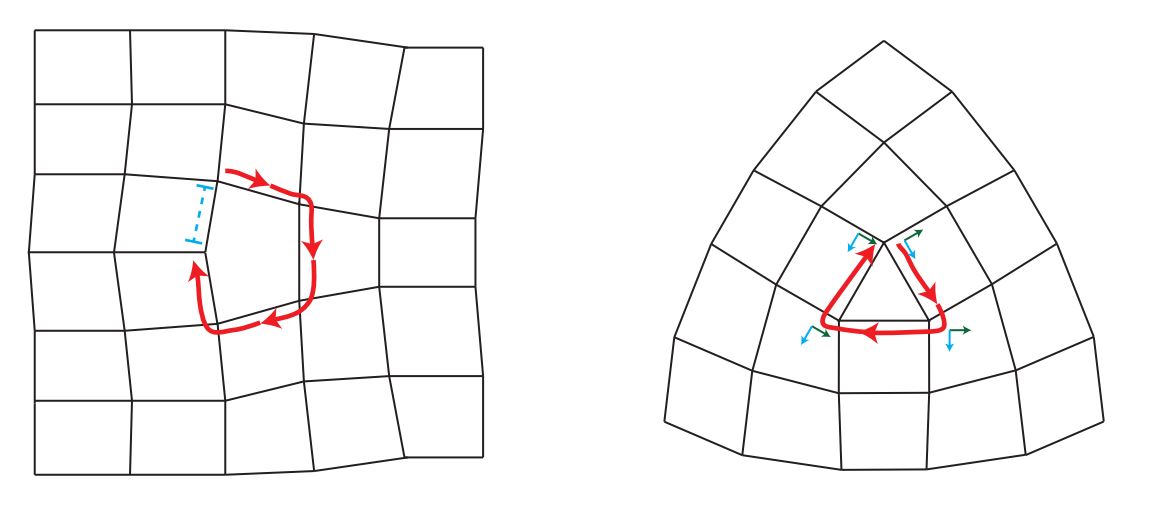
Now this is where the confusion comes about. Since in the first order formalism we have two independent degrees of freedom, we have to make a choice as to how to define variational quantities. For example, traditionally the energy-momentum (EM) tensor is defined as the variation of the action with respect to the metric. But now instead of the metric we have the frame and the torsion. We can choose to define the EM tensor as the variation of the action with respect to the frame while keeping the torsion fixed or we can define it as the variation of the action with respect to the frame while keeping the connection fixed. These are both valid. However, there is only one choice which reduces to the definition of EM in the second order formalism in a manifold with no torsion and that is (understandably) when using the variation while keeping the torsion fixed.
In short, if you are working in the first order formalism and want to look at the effects of torsion, you must consistently choose your definitions such that they give the expected second order results when restricted to torsion-less backgrounds. This was the mistake that lead to the confusion regarding the relationship between torsion and Hall viscosity, which hopefully is now clarified.
