The Power of Symmetries
In Physics, the presence of any kind of symmetry in the system leads to simplifications of the description. For example, translation invariance leads to momentum conservation. In the realm of field theory, there are theories that are endowed with what is called conformal symmetry which can be thought of as the largest generalization of the Poincaré symmetries. The conformal symmetries put great restriction on any theory where they are present. This is epitomized in two dimensions, where the conformal group is infinite dimensional and even leads to theories which are fully determined by these symmetries alone. These are known as minimal models.
Schrödinger Symmetry
In the last few years, the Schrödinger algebra has gotten a fair bit of attention. The Schrödinger symmetry can be thought of as the non-relativistic version of the conformal group; in fact it can be derived from the conformal group through a simple dimensional reduction along a light-like direction. This symmetry group is of great importance as it emerges in some very interesting condensed matter systems. The so called system fermions at unitarity is one such example.
The goal of our recently published paper is to analyze whether or not the Schrödinger group can have consequences similar to the conformal group. For example, are there non-relativistic minimal models where the entire structure of the theory is determined by the algebra alone? To proceed, we take the well established methodology of the analysis of the conformal group. We can form raising and lowering operators, define primary operators and their descendants that can be generated by using the raising operators and consider the commutation relations the various operators.
To look for clues about any possible minimal models, we look for <i>null </i>states which are kind of like rogue family members. These states are generated from the primary operator via the raising operator but no longer go back to the primary using the lowering operators. Their existence is a pathology in the theory which can be only cured by severely restricting the parameters of the theory. The proliferation of null states is how minimal models come about.
In the case of the Schrödinger symmetry, there is a single null state and it is generated by acting the Schrödinger operator on an appropriate primary state. This implies that these primaries satisfy the Schrödinger equaiton and has some very interesting consequences. For example this answers a puzzle about a correlator that was previously calculated and mysteriously seemed to have some unexpected properties. However, because there is only one such null state, there is no analog of minimal models in this non-relativistic context. The Schrödinger symmetry is simply not as powerful as the full relativistic conformal symmetry.
A Peculiar Family and Alien Operators
One very interesting aspect of the Schrödinger algebra is that on a particular subset of the operator space, the raising and lowering ladder operators of the algebra become degenerate. Specifically, the ladder operators commute when acting on operators that carry zero particle number. This commutation relation leads to a very interesting family structure on the zero particle number subspace of the theory.
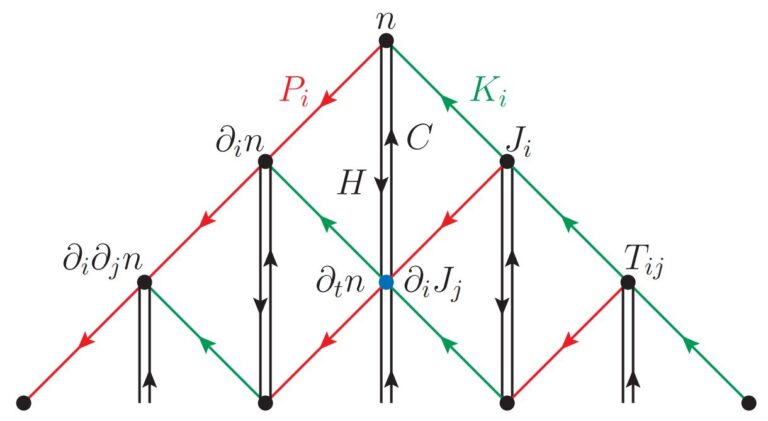
There are specifically two consequences of this strange commutation relation. First, there are operators which are not descended from the family, but they show up in the family tree. We call these alien operators (my adviser also suggested the name in-laws!). In the diagram above, the operators on the far right (the current J_i and the stress tensor T_ij) are alien operators.
The second consequence of the commutation of the ladder operators is that there are spots on the family tree that are occupied by more than one operator. In the diagram above, the orange dot denotes one such position. Since it can be arrived at in two ways: 1. from n using the H raising operator and 2. from J using the P raising operator. And remember that J is in fact an alien operator and is not descended from n. This co-occupation of the same spot on the tree leads to an infinity of conservation laws. From the orange dot we get the continuity equation (density conservation). The next co-occupied point would be to the bottom right and leads to momentum conservation etc. Interestingly, this diagram also demonstrates how these conservation laws would behave if they are ever broken quantum mechanically.
