My adviser Dam T. Son and I recently published a paper showing that the chiral vortical effect (CVE) coefficient is not renormalized. The work is published in the Journal of High Energy Physics (JHEP) and a preprint is available on the arXiv. The proof comes from the generalization of a cute diagrammatic argument by Coleman and Hill. Here is a short summary for non-experts.
The chiral vortical effect (CVE) and the chiral magnetic effect (CME) are the hydrodynamic manifestations of the chiral and mixed gauge-gravity anomaly. In simple terms, they are the weirdness of quantum mechanics making a cameo appearance in the realm of classical physics and because of this they are very cool and fun to study. They were first introduced in 2009 in a paper by Son and Surowka analyzing hydrodynamics in the presence of triangle anomalies. Basically, the CVE and CME respectively say that there is a chiral current parallel and proportional to the vorticity and the magnetic field in the liquid.
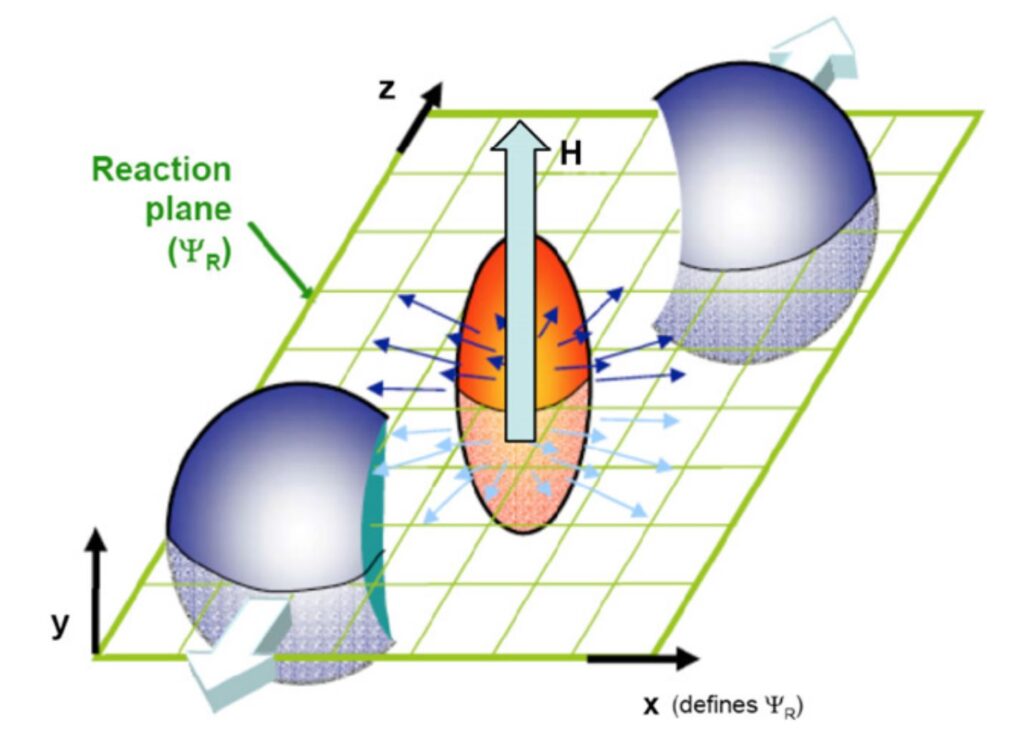
(Almost) all the constants of proportionality are fixed by the quantum triangle anomalies. The image above shows how the chiral magnetic and vortical effects play an important role in the physics of heavy ion collisions (for an updated review see Karzheev 2014).
The interesting thing about the CVE is that there is one term (proportional to temperature squared) in the hydrodynamic description of this effect whose coefficient is not determined by the triangle anomalies. As such we would expect this coefficient to vary from one theory to the next, since there is no reason for it to be fixed. A puzzle remained, however, as it was shown that the coefficient is the same in two very different theories calculated in different ways.
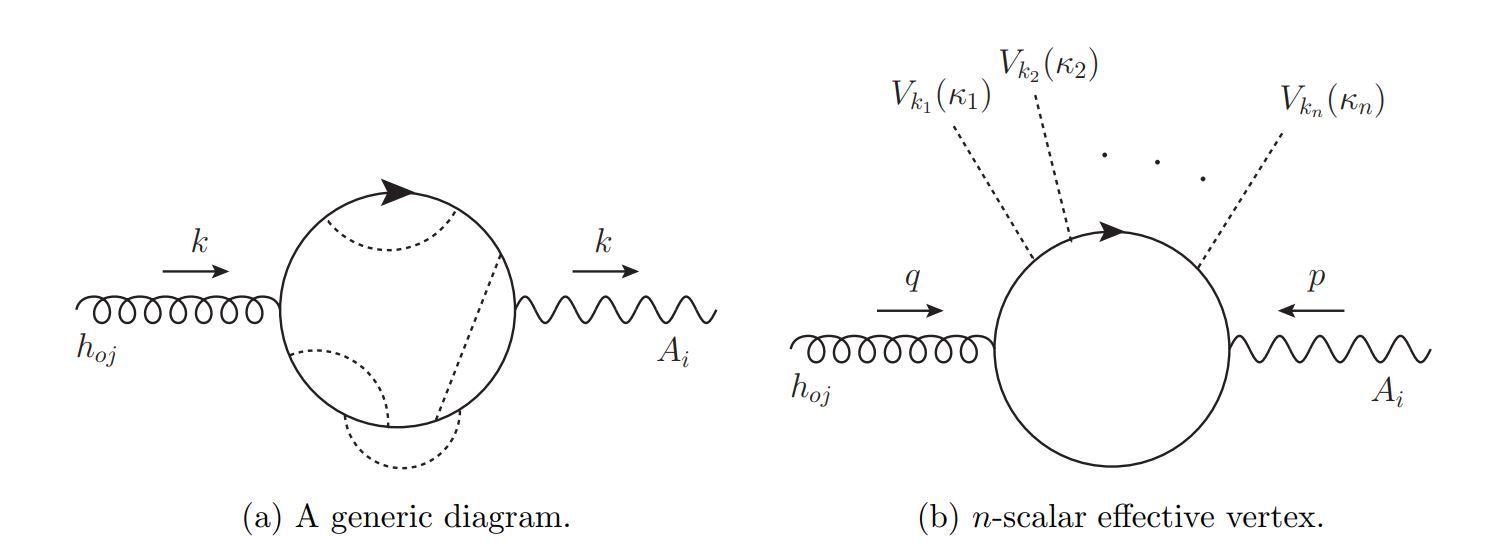
In our recent work, we show that in fact there is an argument using Feynman diagrams that proves that this coefficient remains the same as we change the parameters of the theory thereby solving the puzzle. The diagrams in question are the mixed gauge/gravity correlators which take the generic form in the picture below. The argument is in essence a generalization of the non-renormalization of Abelian Chern-Simons theory given by Coleman and Hill.
Fun fact: The 1/12 factor appearing in the CVE coefficient is related to the following weird relationship:
1 + 2 + 3 + … = – 1 / 12
In other words, the sum of all positive integers is equal to negative 1/12. The reason for this apparent contradiction (sum of positive numbers giving a negative result) is due to the fact that the left hand side is ill-defined (diverges to infinity). Therefore, to make sense of this sum, we need to pull some tricks which in physics we call regularization. In this case, regularizing the sum using the zeta function (or exponential damping) results in the above relationship.
