My collaborator, Matthew M Roberts and I recently published a paper performing a holographic investigation of the topological properties of chiral superfluids. I have always been very interested in physical consequences of topological relationships in different systems. Last year, we discovered a relationship between the Hall viscosity of relativistic quantum Hall systems and a topological quantity known as the shift that relates to the Euler characteristic of the system. The proof of this relationship in that paper is fully analytical but has a few limitations. For example, it only holds at zero temperature. In our recent work, we use holography to extend that analysis to a wider regime of applicability which traditionally is much harder to tackle analytically. The paper is published in JHEP (Journal of High Energy Physics) and the pre-print is available for free on the arXiv.
What is holography?
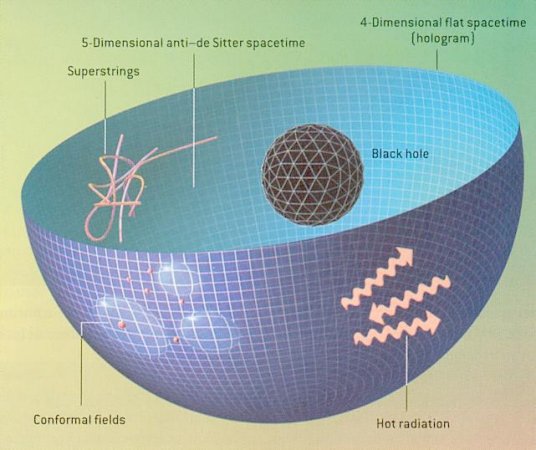
Holography, also known as AdS/CFT correspondence, is the product of work by a number of prominent physicists including Gerard ‘t Hooft, Leonard Susskind, and Juan Maldacena in the late 90s and early 2000s. In very simple terms, it is the statement that a gravitational theory defined in a box can be equally described by a ‘dual theory’ defined only on the boundary of that box. This is highly non-trivial as it implies that the boundary degrees of freedom mirror those of the bulk of the box, therefore knowing what happens on the boundary, is sufficient to describe the details of the happenings inside. This bulk/boundary correspondence is also why this conjecture is called the holographic principle. The image, by Jacob D. Bekenstein and Alfred T. Kamajian is a cartoon of a 5D space-time with a 4D holographic boundary.
An interesting property of the AdS/CFT correspondence, as well as many other dualities in physics, is that it’s a strong/weak duality. What this means is that when one side of the duality is strongly interacting and therefore difficult to deal with the other side is weakly interacting and easy to compute. This makes holography an incredibly useful tool for high energy theoretical physics.
It should be noted that the holographic dual for the real world is not known. It is not even known that this holographic dual exists. However, there are theories that resemble the real world to various degrees and in practice, physicists use these to learn about the real world.
Hall Viscosity and Chiral Superfluids
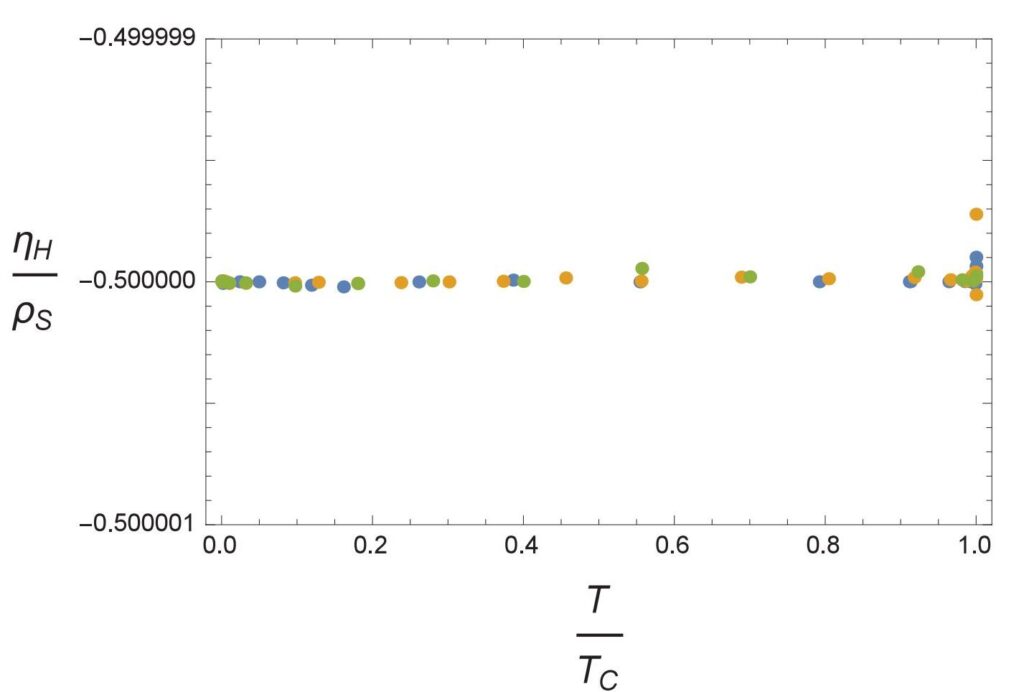
Using a holographic setup we computed the hall viscosity of chiral p-wave superfluids and found that the zero temperature relationship between the superfluid density and Hall viscosity holds at all temperatures. This computation is numerical since the differential equations cannot be solved exactly. The result is given in the next graph. The ratio is equal to 1/2 with an accuracy of better than 1 part in a million! The reason why this still happens to be the case at finite temperature is still not fully known and is the subject of ongoing investigation.